Material properties are very important and first assumption to represent any material model in FEA. If you input wrong material details it will greatly affect your results. If you input garbage in FEA you will always get garbage in output. So you always need to pay attention on what material details you are entering in FEA. Defining any material in FEA is not as complex as representing actual material. Actual materials have various material specifications such as, yield stress, ultimate stress, young modulus, Poisson ratio, bulk modulus, thermal conductivity, elongation, specific heat, stress vs strain curve, electric properties and so on. In FEA, no need to define all the details to model the material, material details required are depend on the FE analysis types you want to perform (linear or nonlinear solution, static or dynamic analysis, steady state or time dependent, etc.).
The following table represents the minimum material properties required as per basic FE analysis types.
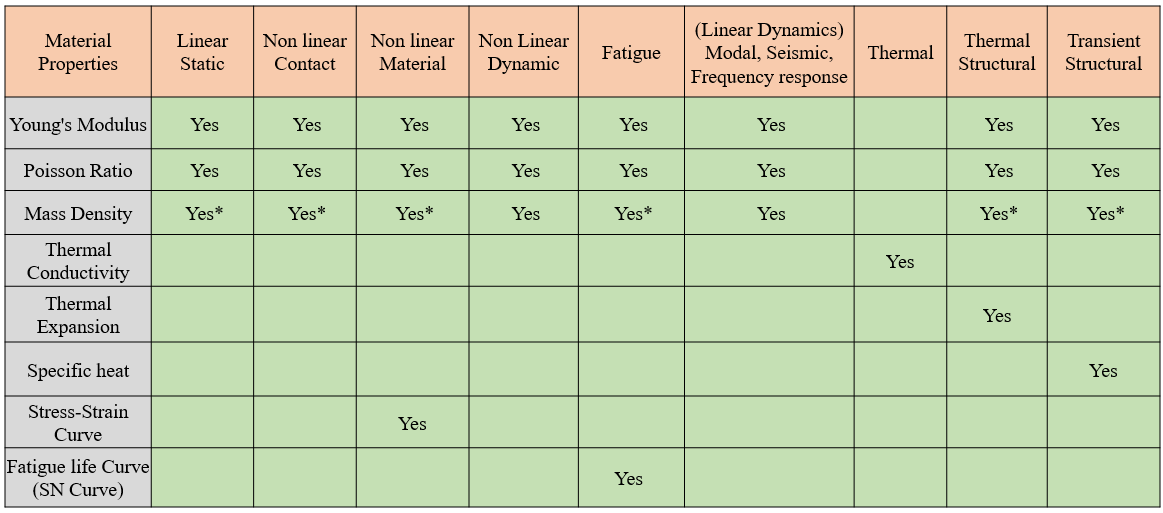
* is marked for mass density for few analyses. The mass density only required if you have mass elements in the analysis. These mass elements are used to apply weight of the components which are not modelled in the analysis. By adding mass density and applying standard earth gravity (acceleration), the effect of point mass (applied on mass elements) is taken into account.
Two material properties you will always need to define except thermal for the material. The first one is young’s modulus and the second one is the Poisson ratio.
Young’s Modulus:
Young’s modulus or Modulus of elasticity (in tension) is a mechanical property that measures the tensile stiffness of a solid material. Young’s Modulus is basically the slope of the straight elastic part of the stress-strain curve as shown in figure 1. It is denoted by letter E and its values are so large that they are expressed not in Pascal’s but in gigapascals (GPa/MPa).
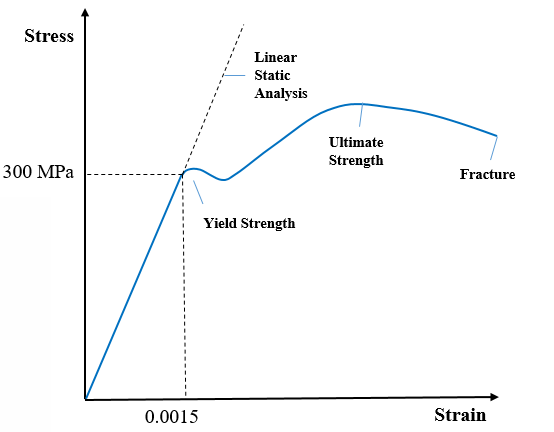
Linear static analysis applied to the majority of FEA models follows the principle of Hooke’s Law of elasticity. I.e. the stiffness of the part follows the elastic portion of the stress strain curve.
Majority of FE analysis is linear elastic one which follows the hook’s laws while for nonlinear material you will need additional stress vs strain curve.
Form figure 1 you can easily calculate the young’s modulus.
Here, yield stress, σ = 300 MPa
Strain at Yield, ε = 0.0015
Young’s Modulus, E=
E = 200 GPa.
Poisson’s ratio:
Poisson’s Ratio is a measure of the Poisson effect, the deformation (expansion or contraction) of a material in directions perpendicular to the direction of loading. It measure of the lateral contraction of a material when under tensile stress in the longitudinal direction. Most materials have Poisson’s ratio values ranging between 0.0 and 0.5. Incompressible materials, such as rubber, have a ratio near 0.5.
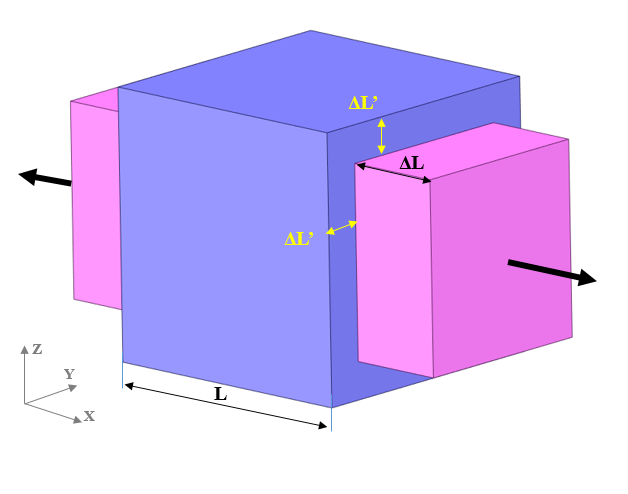
Figure 2 shows Solid cube with length L having linear elastic material & 0.5 Poisson ratio subjected to tensile pull force on either sides of the cubes. Due to pull force the blue cube deform to new expanded position as shown by pink colour. Due to force application, cube expands in ΔL due to tension in x direction, and contracted in Y-Z directions by ΔL’.
For nonlinear analysis, you need to define stress vs strain curve, but there are few nonlinear analysis where you will need additional material details are discussed below:
Bilinear or Multilinear Isotropic Materials:
To define bi-linear materials you will need yield strength and tangent modulus. Once you define yield strength and tangent modulus in your FEA software, it will automatically plot the stress strain curves. Bilinear material are as define as elastic plastic and perfectly perfectly plastic.
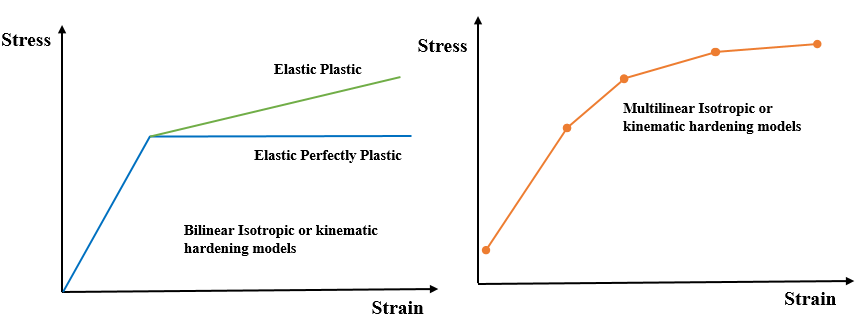
Figure 3 shows bi-linear and multilinear isotropic of kinematic hardening models materials. First graphs shows bilinear material such as elastic perfectly plastic (To model elastic perfectly plastic, you need to input yield strength and tangent modulus as zero value) and elastic plastic materials. second graph shows multi linear isotropic and kinematic hardening materials. (Refer our blog-post to define bilinear and multilinear materials….coming soon)
Gasket Nonlinear Materials:
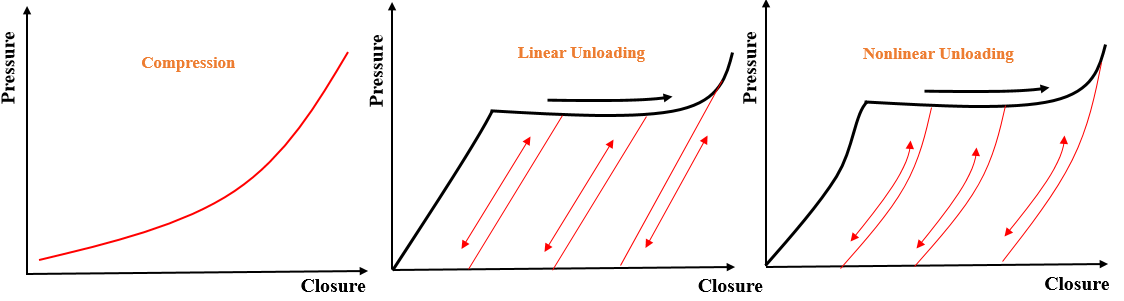
To perform the gasket analysis you need to model the gasket behavior through loading (compression) and unloading curve. Refer figure 4, first graph shows the compression curve (you need to define the closure (in/mm) vs pressure (psi/MPa) the second & third graph shows the linear and nonlinear unloading behavior. You will get this data from manufacturing catalog. Also additional user define limits on tensile and shear stress gasket can also be inserted.
Hyperelastic Material:
If you do not have gasket material details, then gasket can also be simulated with the help of hyperelastic material modeling. There are various method to model hyperelastic material such as Neo Hookean, Ogden & Yeoh method, Mooney and Polynominal methods, etc. The simplest one is Neo-Hooekan method; In this method based on gasket shore hardness the two material constant are calculated (Initial shear modulus, Mu & Incompressibillity Parameter, D1). Once you insert these constants in FEA software, it will automatically generates stress strain curve.
Summary:
-
No need to define all the material detail to model material in FEA. Table 1 present the material required as per analysis types.
-
Young’s modulus and Poisson ratio are majority used material detail for any FEA analysis types except thermal analysis
-
Elastic perfectly plastic material is define by entering yield strength value and tangent modulus as zero.
-
Gakset behavior is model by defining compression curve as well as linear and nonlinear unloading curves.
-
Gasket material can also modelled by simplest Neo-Hookean method.
