As we discussed in (What is nonlinear Analysis?) the nonlinear solution is not as simple as linear solution, it involves most of FEA related issues such as solution is not converging, solution taking too much time, contact abrupt changes, displacement converging but moments does not or wise versa. Then the question come how does solver solve this nonlinear simulation? In this blog we will discuss one of the method to solve nonlinear analysis. ANSYS mechanical uses the same method for calculation of nonlinear simulations.
Newton Raphson Method:
As we know that, linear equations does not gives the response for nonlinear analysis. However, iterative series of linear approximations with corrections can be used to analyse the nonlinear structure. This iterative process of equilibrium iteration called Newton Raphson Method.
In case of nonlinear simulation, the stiffness of the structure is not constant with respect to loading (force versus displacement plot is not as straight line). This changes in stiffness are mainly due to nonlinear material (material does no obeys hooks law, material plastically deform after elastic limit), nonlinear geometry (large deformation due small or larger loads) or Contact nonlinearity (contact status changes abruptly). In such nonlinear scenarios, sudden changes in any aspects (like whole load application in single step) may cause convergence difficulties. And hence the loads are need to apply gradually to avoid convergence issues.
Let’s discuss through simple example as shown in graph.
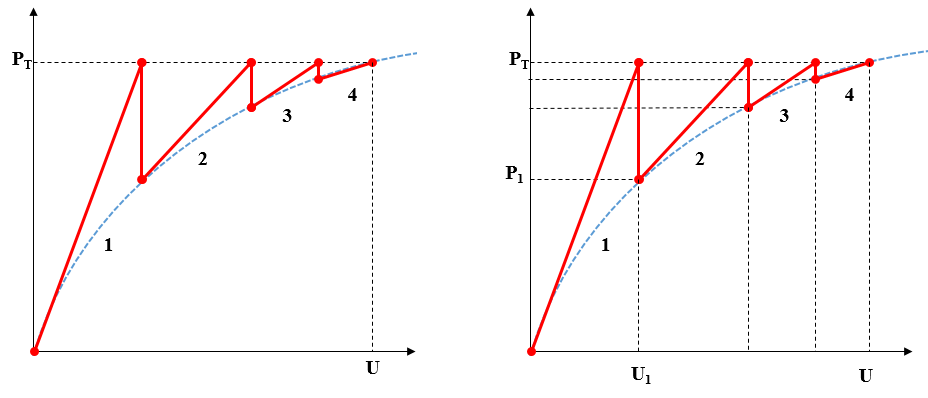
Figure 1 shows the curve (in blue colour) represent forces vs displacement relationship, here vertical axis shows the forces while horizontal axis shows the displacement. Newton Raphson method is iterative process, but how does it perform the iterations ?
In this method the total load is applied in first iteration…..as a result of which solver gives some displacement U1 which calculates the internal forces as P1, then system try to establish equilibrium, but if P1≠ U1, then it results is non equilibrium condition, hence further it split the total force (slope of dotted line) and calculate new stiffness matrixes until equilibrium is not achieved…likewise it perform the iteration 1, 2, 3 & 4 and then equate with internal forces (P1, P2, P3 & PT) thus when the internal force matches with total applied forces, equilibrium is achieved and solution is said to be converge.
Here the difference of PT – P1 is residual forces (out of balance). So it is necessary to have smaller residual force so that solution will converge.
Let’s discuss further with below example:
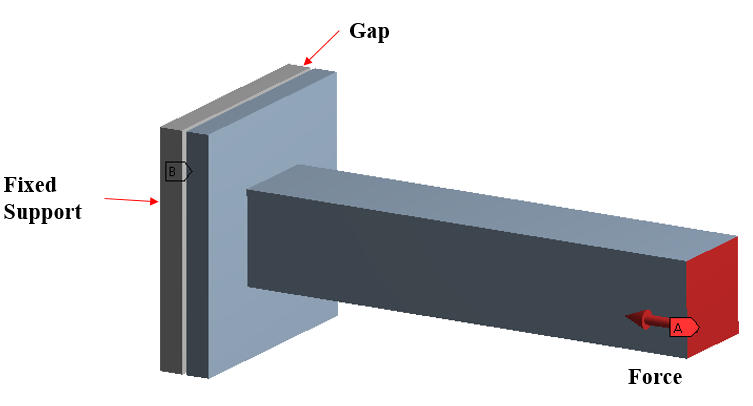
Figure 2 shows the two rectangular plate, one plate is fixed in all dof and other plate is attached to horizontal beam where the force is applied. This horizontal force on the beam will cause the plate to move right side and get in contact with other plate & thus contact will established and solution start converging. Here the challenge is that, you need to establish nonlinear contact between the plates but when you apply whole force in single step, it will results in non-convergence issue.
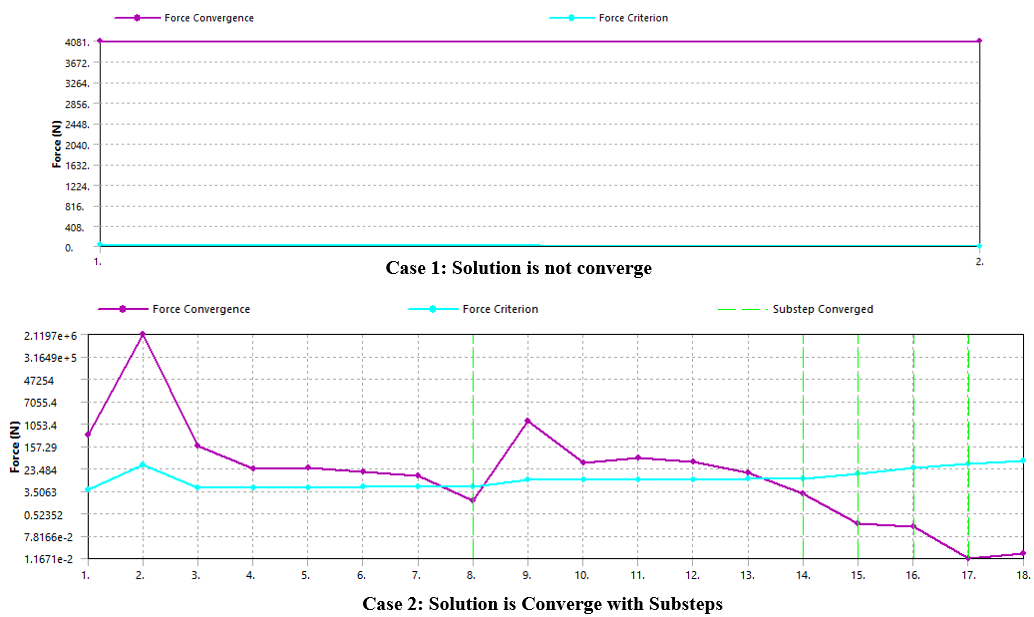
Refer figure 3, case-1 shows not convergence (this is due to load applied in single step) and refer case-2, where load is applied in different load steps resulting force convergence meets the force criteria (Internal force). So instead of applying load in single load steps, if you apply load gradually will help to achieve the convergence.
Newton Raphson Method Convergence Techniques:
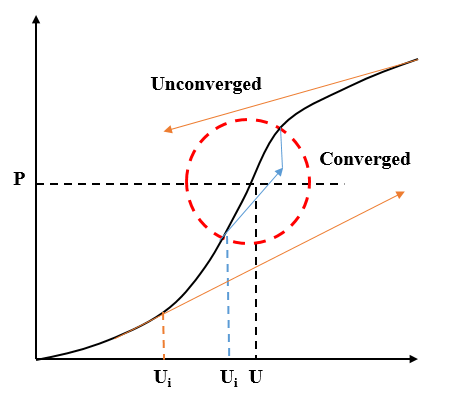
As discussed above Newton Raphson achieve the convergence, but the fact is it does not achieve in all the cases. It will achieve only if the starting configuration is inside the radius of convergence. Figure 4 shows that when Ui start within convergence radius, the solution get converge but if Ui starts to far from convergence radius then it does not converge and start diverging.
Following techniques are useful to achieved converge solution:
- Apply load incrementally as discussed (refer figure 2, case 2)
- Use convergence enhancement tools to increase radius of convergence.
- Nonlinear contact settings such as interface treatment, stabilization damping factors, etc.
You can achieve convergence with above methods but you need to always make sure that it will not affect the accuracy of the solution.
References:
- ANSYS Help Manuals, 17.0
