It is quite simple and straight forward compare to other analysis types, as name suggest
- Linear means FE solver uses linear stress vs strain curve and
- Static means which does not change with respect to time.
Let’s discuss furthermore in more depth….
Linear means FE solvers uses linear stress strain curve i.e. straight line from initial to deformed position. Refer Figure 1 for stress strain curve, the linear material behaves as straight lines from origins. It means it obeys the hooks law, σ = ε * E is the equation of a straight line (y = m x) passing through the origin. FE software follows the linear path for calculations while in actual the material behaves nonlinear after the yield point.
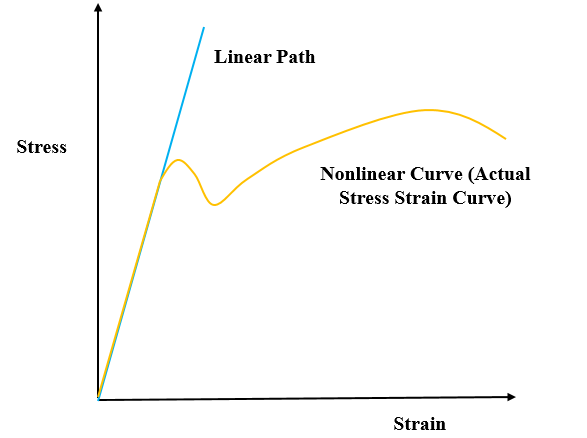
In real life scenario, the stress strain curve no longer straight line after yield point, it behaves as nonlinear curve after crossing yield and material will fail or break after the ultimate point while in case of linear FEA, you will no longer see the failure but you can see the region with high stress (failure location) in red region. Furthermore you can specify the red color zone above yield limit from legends. Likewise FEA engineer identifies the failure location and concludes the analysis based on yield or ultimate limit criteria.
When we say static means it should obey the two conditions, the first one is loads are constant with respect to time (for example dead weight) the second conditions the summation of forces and moments are equal to zero. FEA should fulfill this condition at each and every node thus in FEA the applied external forces and moments should be equal to the reactions obtained from FEA simulation.
How does linear solver solve the FEA problems?
The basic finite element equation to solve linear static equation is:
F= K*D
Here,
F is force (loads applied to the structure)
K, is stiffness matrix, (Characteristic properties of elements) &
D, is displacement (usually unknown)
- Once FEA model is ready, the numerical methods solve the matrix for unknown displacements based on force and stiffness matrix. The stiffness matrix is singular until few constraints are applied to avoid the rigid body motion.
- The unknown displacement are solved using a Gauss-Seidel method or gauss elimination method by direct solver. (Iterative solver can also be used but it is useful for nonlinear analysis where convergence need to achieved)
- Hooks law (σ = ε * E) is used to calculated the stresses. E is elasticity (matrix) of the material and strains are the functions of displacements. Linear material obeys the hooks law where the deformation are in the elastic range, the stresses are assumed to be linear function of strains.
- Integration is used to get the displacement and interpolation to get the stresses in FEA model. (Stresses are calculated at the nodes and interpolation are used for stresses on elements path, surfaces or volume of FEA model)
So overall with linear static analysis:
- The material considered is elastic
- The loads does not change with respect to time
- Due to linearity it does not go under large deformation (Small deformations values compare to nonlinear analysis).
Practical Applications: Linear static is most widely used analysis due to faster response and unavailability of nonlinear materials. Most of industries like offshore, automobile, aerospace, oil and gas industry, civil & structural engineering industry perform the linear static analysis.
