What is Nonlinear analysis ? Types of Nonlinearity

The nonlinear is very important term in FEA. Most of engineer gets stuck in this topics as it is not simple as linear simulations. In case of nonlinear simulation you need to patient, have sound knowledge of FEA nonlinearity (like material behavior, geometric & stiffness changes during load events). Most of FEA related issues you will find while simulating nonlinear simulation such as solution is not converging, solution taking too much time, contact abrupt changes, displacement converging but moments does not or wise versa. Just changing linear to nonlinear zone is not enough, you will need to decide the load step increments, solver setting, and various contact setting. Overall based on nonlinearity type, you need to work on nonlinear setting given in the FEA software’s. In this blog we will discuss the types of nonlinear analysis, types of non-linearity and nonlinear FEA issues.

As name suggest, nonlinear means the force versus displacement plot is not as straight line. The stiffness of the structure is no longer constant but varies with respect to loading.  Majority classes of structures does not have linear relationship between force and displacement. A structure is said to be nonlinear, if the loading causes the significant changes in the stiffness. Typical reasons for stiffness changes are:

• Material does no obeys hooks law, material plastically deform (strain) after elastic limit.
• Large deformation due small or larger loads (loaded fishing rods)
• Contact status abrupt change

Types of Nonlinearity:

There are three basic source of nonlinearity; the first one is geometry based nonlinearity, second one is material based and third one is contact (& boundary condition) based nonlinearity. Figure 1 shows the types of non linearity.

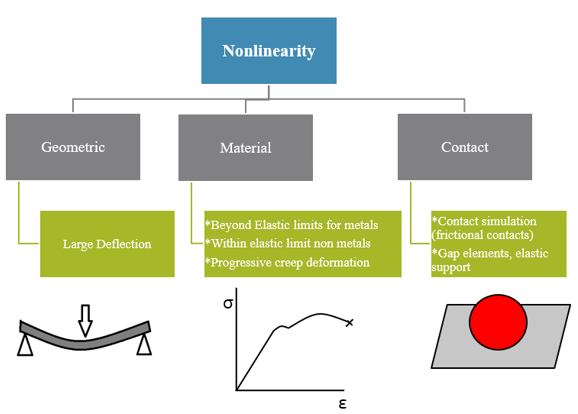
1. Geometric Nonlinearity:

The changing geometric configuration due to large deformation of the structure cause nonlinear behavior. Geometric nonlinearity is not only because of large deformation but also due to large strain & large rotation too. The geometric nonlinearity causes to change in geometry cross section due to large deformation. Geometry buckling is also cause of geometric non linearity, in case of buckling huge compressive load causes the structural member to buckle resulting higher displacement.

Here the questions comes, How to decide whether the analysis is linear or nonlinear?

In linear geometric analysis, the deformations and rotations are smaller like within 5 % as generic rule, but in case of nonlinear geometric analysis, displacement and rotations are large. Small changes in magnitude of force for nonlinear geometry, can change convergence behavior considerably. However the geometric nonlinearity is not only due to large deformation/rotation but varies based loading and situation too. Consider example of buckling of shells which happen with small initial displacements but under a very nonlinear behavior. It happens in small displacements and deal with membrane or axial loads. In FEA software geometry nonlinear is solved simply by keeping nonlinear zone on.

It is difficult to predict the case of geometric nonlinearity, as it needs lot of experiments and judge the case by looking the scenario.

2. Material Nonlinearity:

In real world all engineering material are inherently nonlinear but we can idealize by accounting only certain effect which are important for analysis. The linear materials is most simplified material type. The other type is nonlinear elastic if the deformation is recoverable and plastic if deformation is permanent.

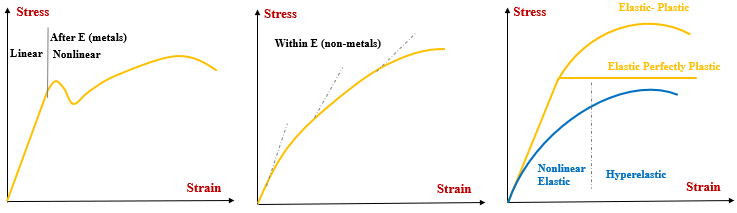
Figure 2 shows the stress strain curve for metal, non-metals & nonlinearity features. In case of metals, material moves to plastic zone after elastic limit, while non-metals have nonlinear stress strain curve (plastic, asbestos, fibres, etc.) from origin itself thus in both the cases curve shows the source of nonlinearity. Nonlinear curve helps to input exact stress vs strain after the yield point which gives the exact results. Furthermore creep also considered as nonlinear phenomenon, at maximum temperature, even for small magnitude loads, kept applied for longer period of time, would cause failure. 

Few Major nonlinear material (behavior) classification:

1. Nonlinear elastic
2. Hyperplastic (example gasket (rubber) material)
3. Linear elastic perfectly plastic
4. Elastic perfectly plastic
5. Elastic time dependent plastic (creep)
6. Strain & temperature dependent elasticity and plasticity.

Stress strain curve usually obtained from tensile test in labs and you might experience some struggle to find out the actual strain stress curve for the material you are analyzing. In that case you can refer some research papers or free internet source like Matweb, etc. you even can assume the curve of equivalent material and complete the simulation instead of giving up. In FEA you will put stress vs strain curve as material input and then FEA calculates the deformation and calculates the strain for those deformations. And then FEA uses material stress strain curve to translate stain into stresses.

3. Contact Nonlinearity:

In contact nonlinearity abrupt change in stiffness may occur when bodies come into or out of contact each other. This type on nonlinearity is used to simulate the gap between two parts. While defining contact between two bodies, you need to decide whether it carries the friction or not. Friction coefficient can be used to decide the amount of resistance between the contact bodies. The selection of friction coefficient affects the contacting surfaces behaviour and hence the friction coefficient is selected based on dry or lubricated friction, contacting material, etc. Sometimes boundary conditions can also be treated as nonlinear analysis like elastic support.

Rubber boot seal is an example of nonlinear geometry (due to large strain and large deformation), nonlinear material (rubber) and changing status nonlinearities (contact).

Nonlinear FEA Issues:

• Achieving convergence: Obtaining convergence is biggest challenge in nonlinear analysis.
  • Trial and error is sometimes required.
  • Complex problems might require more load increments, and many iterations at the each load step to achieve the convergence.
• Balancing expenses versus accuracy
  • FEA involves expenses (Solution time, disk and memory requirements)
  • More detail and a finer mesh generally lead to a more accurate solution, but require more time and system resources.
  • Nonlinear analysis need additional iteration affects both accuracy and expenses.
• Verification
  • Difficult to verify the FEA results due to increased complexity of nonlinear behaviour.
  • The sensitivity studies (mesh convergence, increased mesh density, reduced load increments, varying other model parameters) become more expensive.
• Results of the nonlinear analysis cannot be scaled.
• The structural behavior can be markedly non-proportional to the applied load.