All the real life objects are continuous which are made up of various small particles, molecules & molecules of atoms. As per material science all these small particles are connected with each other by force of extraction. All are glued or bonded with each other’s, it means there is no physical gap exist between two particles. Analyzing continuous real life object is difficult due to the fact that it contains infinite particles results in infinite degrees of freedom for the solution. And hence numerical method (FEM) are used to simplify the object by discretizing. In simple words, discretization of continuous system with infinite degrees of freedom to a finite degrees of freedom which is called as meshing. Meshing splits the continuous object into small parts called as finite elements and points joining finite elements are called as nodes. In other words, nodes work like atoms and the gap between the nodes is filled by an entity called an elements. Thus the continuous object is represented by equivalent finite elements system.
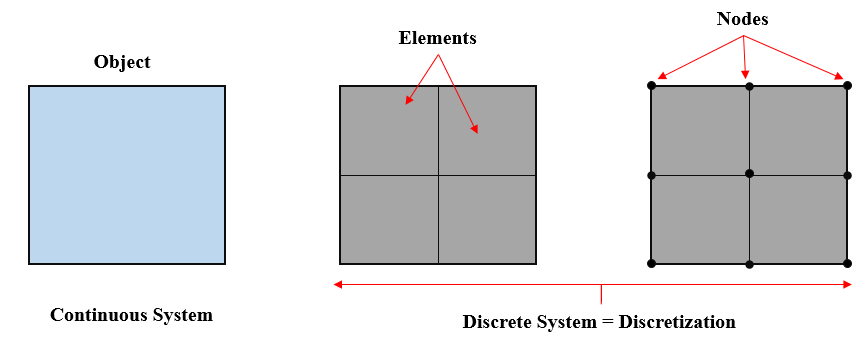
You might have understood what discretization, what is meshing is, but still you are looking for the answer of Why do we carry out the meshing, What is the purpose of meshing?
In simple words, in order get the solution of problem we use FEM numerical method and it does calculations at limited (finite) number of points with the help of meshing and then interpolates results for the entire (surface or volume) domain of your problem. So in order to analyze the whole problem we use meshing.
As we know that meshing is used to convert continuous system to limited number of finite points, but the next question will come in your mind is that,
How many point (nodes and elements) should we consider ? How is the accuracy?
Let’s us consider simple example of circle (Refer figure 2), you can put 3 lines in circle area then increase the number of lines to 4, 8, 16, 32 and 64. You will find that, by increasing the number of lines you will move closer to circle area. With 3 lines you are not able to capture the circle area, as you increase the number of lines, your error margin reduces and increase the accuracy.

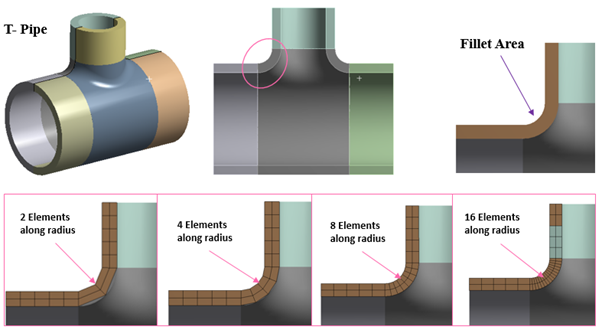
Let’s discuss furthermore practical example of T pipe fillet region. Figure 3 shows the mesh for fillet region of T pipe, check the highlighted fillet area with 2, 4, 8 & 16 elements respectively. When 2 elements are presents at fillet region, the fillet curvature is not captured properly but as you go on increasing the number of elements, you will find mesh captures the curvature of fillet area. So it is clear if we put more and more elements you will move more closure to the geometry (Captured properly geometrical features like fillet, champers, holes, etc.). Also FEA perform the calculations at nodes, if more number of nodes (elements) means increased calculations points and thus finer mesh captures correct geometrical stiffness as well as increases the calculations points, which results in higher accuracy. In simple words, Higher the number of nodes & elements, higher the accuracy.
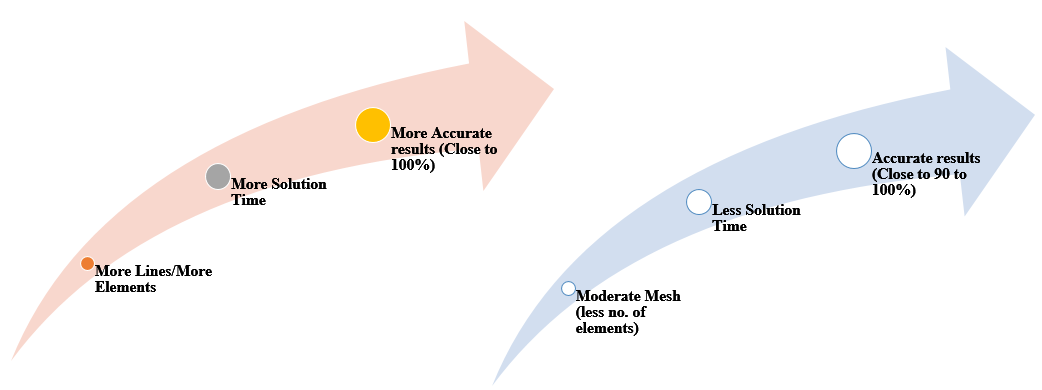
Then another questions comes….. Why always does not consider fine mesh size & higher node count?
The reason behind it is that, as we increase the number of nodes, dof increases and thus solution time increase. (Refer FEA solution time depends on total number of dof of the system to be Analyze) as solution time is directly proportional to number of dofs. If results are taking longer time then it will affect the product life cycle, design modifications time will increase, in addition to that the cost of running the simulation will increase. So instead of very finer mesh, the FEA analyst prefer to select moderate mesh size so that the solution time will be reduced without affecting much accuracy. Your engineering judgement, the product analysis experience (for example if you are manufacturing the same pressure vessel for years, based on your past experience you can easily decide the mesh size for all the new vessel and for their respective nozzles) & mesh convergence study will help to select the moderate or optimum mesh size.
Summary
The discretization & mesh is important parameter in FEA.
The selection of mesh size affects the solution time.
Moderate mesh with reasonable accuracy is more preferable.
Mesh convergence study can be used to decide the mesh size.
